My research is in mathematical relativity and black hole physics.
What is general relativity?

The notion of time in general relativity is almost, but not quite, entirely unrelated to that depicted in Salvador Dali's "Persistence of Memory".
General relativity (or "GR" for short) is Einstein's theory that says that space, time and gravity are very different from what our intuition and Newtonian physics suggest. Though causality is always preserved, there is no universal "flow" of time. In particular there is no invariant way to define generic instants of simultaneity across the universe and different observers may (and usually will) measure different intervals of time between the same events.Meanwhile, gravity is not really a force but rather a manifestation of the curvature of four-dimensional spacetime. Objects that we think of as moving under the influence of gravity (for example planets around the sun) are actually moving along "straight" lines in the curved spacetime. As strange as this sounds to someone who learns of it for the first time, GR is one of the basic building blocks of our modern understanding of reality and is fundamental to an understanding of the origin to the ultimate end of the universe - and everything in between. GR is the theory that predicted the Big Bang, the expansion of the universe, black holes and gravitational waves.
What is a black hole?
Black holes are probably best known as supernova remnants - when a large enough star exhausts its fuel and explodes, the left-over core collapses to a singularity under the weight of its own gravity. However, this gravitational field is so strong that not even light can escape its pull and so the singularity is concealed from the rest of the universe inside a black hole. Such black holes began as theoretical predictions but over the last couple of decades the observational evidence for their existence as real astrophysical objects has become very strong and is getting better every year. Binary systems including black holes are widely expected to be some of the brightest sources of gravitational waves and based on these expectations gravitational wave observatories have been built all over the world. Apart from these stellar mass black holes however, there are also supermassive black holes at the centre of most galaxies which can have masses millions or even billions times that of the sun. The best studied of these is at the centre of our own galaxy and is relatively unassuming, but in the early universe these giants powered quasars. Black holes are fascinating and important astrophysical objects.
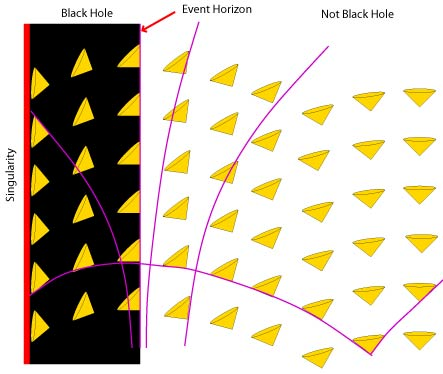
The spacetime diagram above illustrates a black hole from a geometric point of view. Time is on the vertical axis and space is on the horizontal axis. The little yellow cones are light cones which represent all the allowed paths of light from a point in space-time. Spacetime curvature tilts those cones towards massive objects and inside the black hole curvature is so great that all paths lead deeper into the hole and towards the singularity.
Aside from these (and other) applications, black holes play an important conceptual role: as extreme objects they demonstrate just how different the Einstein picture of spacetime and gravity is from the old-fashioned Newtonian view. For example the lack of a universal flow of time is demonstrated by apparent paradoxes that arise when considering black holes: an observer far from a black hole looking at the watch of an infalling astronaut would see time slow to a stop as she approached the horizon. However, this doesn't mean that time stops for the astronaut. Though she'd feel huge tidal forces trying to rip her apart, she would notice nothing unusual about the flow of time as she fell through the horizon. Time would continue to flow normally for her until she reached the singularity at the centre of the hole - at which time it would end! A bit of careful thought shows that any apparent contradictions in this picture can be resolved by abandoning the notion of universal instants of simultaneity.
That all sounds like physics. What are you doing in a math department?
Enough generalities. What specifically do you do?
As I've mentioned a couple of times most of my work is in mathematical black hole physics. I am especially interested in dynamical black holes and their properties, both for their own sake but also to help develop tools that might be useful in better understanding the astrophysics observed in numerical simulations of black holes. Black holes have geometric signatures whose properties can be studied using the Einstein equations - this is what I spend a good chunk of my time doing and is fairly abstract, mathematical work. However, both to build the intuition to know what to look for and also to confirm theoretical predictions, it is also important to study actual solutions and I (and my students) also spend time studying exact solutions, perturbations of those solutions, and recently we've started to do a little bit of numerical work. For more details check out our papers or drop by to talk to me - especially if you're looking for a summer, honours or graduate project in relativity, gravitational physics, or differential geometry.

