Heron or Hero was a Greek Mathematician who discovered a formula for the area of a triangle, with sides

Before giving this formula, we need a little trigonometry. We assume that you are familiar with some trigonometry, and know what is meant by the ``sine'' and the ``cosine'' of an angle. Consider with a right angle at X and let .

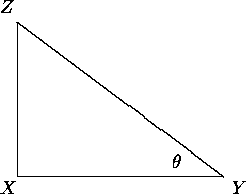
We define 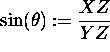and .

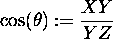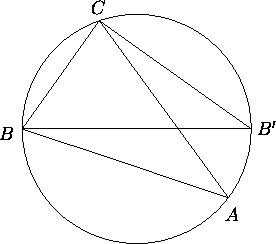
Join CB', and note that

Further, note that is a right angle. Observe that

where, as usual, we denote BC by a.Then

This shows that

and so the Sine Rule is obtained.

Consider and draw the perpendicular line to AB through C. Suppose this line meets AB at D.

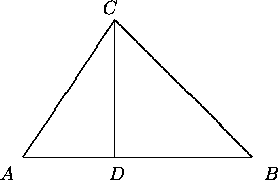
Then

so that

and

From this, by squaring the latter two equations, we get:

Adding these together gives

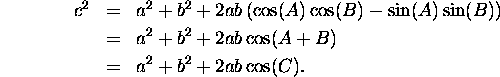
This is the Cosine Rule.

Since we have found that

we can deduce that

We shall use the Sine Rule to get an new formula for the area of a triangle.

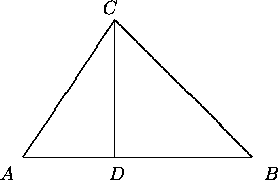
The area of is given by base height. Thus

The perimeter of is given by AB+BC+CA. The semi-perimeter is half of this value! We denote the semi-perimeter by s, so that

We use equations (1) and (2) to get

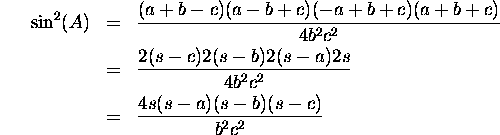
A similar argument gives

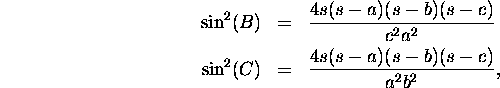
and so

Using the formulae for the area of a triangle and these, we get

This is HERON's formula. The great advantage is that the area of the triangle can be calculated solely from the knowledge of the lengths of the sides. No information about the angles is required.

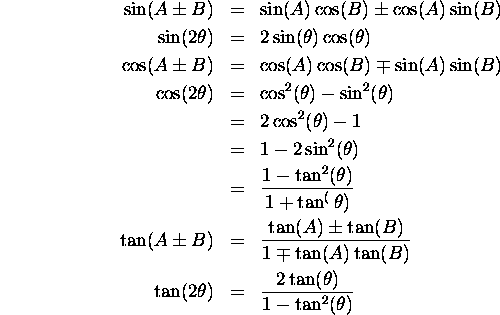
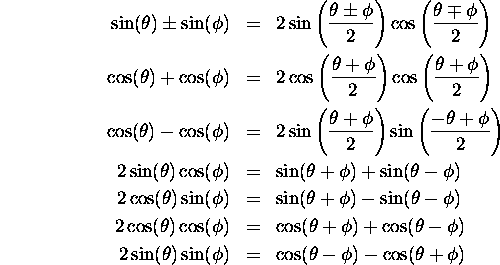
Here we give an algebraic derivation of Heron's Formula.

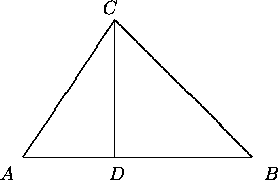
Let CD=h, AB=c, BC=a and CA=b as usual. Then

so that

giving

Squaring gives

or

or

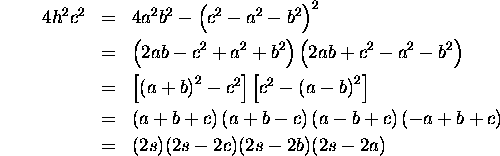
and Heron's formula follows at once.

Here we extend Heron's formula to find the area of CYCLIC quadrilaterals.Consider the cyclic quadrilateral ABCD and denote the sides and a diagonal as follows:

We define 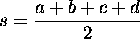. Let , so that .

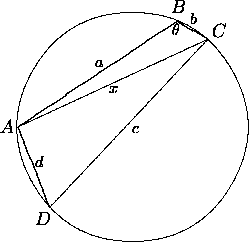
Then, the cosine rule, applied to and , gives that

Eliminating from these equations gives

Thus

yielding

Let represent the area of and represent the area of .Heron's formula then gives us:

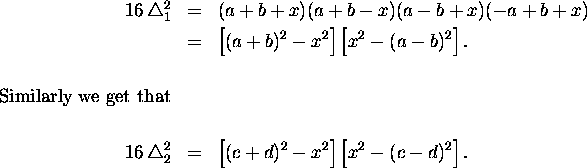
Now

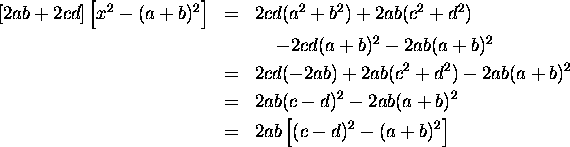
Similarly

Together, we now get

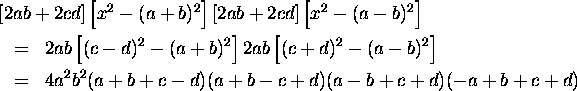
so that

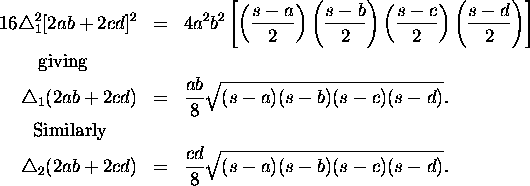
From this it is very easy to obtain the following formula for the area of a cyclic quadrilateral: