|
Biography: Dr. Jahrul Alam is a Professor of Applied Mathematics at Memorial University, cross-appointed to the Department of Physics and Physical Oceanography. He earned his Ph.D. in Applied Mathematics from McMaster University in 2006, specializing in turbulence modeling. Following his doctoral studies, Dr. Alam served as a SHARCNET Postdoctoral Fellow in atmospheric modeling at the Department of Earth and Environmental Sciences, University of Waterloo, and as a visiting scholar at the Department of Atmospheric Sciences, National Taiwan University.
Since joining Memorial University in 2008, Dr. Alam has made significant contributions to the field of Computational Fluid Dynamics (CFD). He has taken on several leadership roles, including serving as Chair of the Scientific Computing Program at Memorial University and as an Associate Editor for the journal Nonlinear Dynamics (published by Elsevier). His research focuses on the application of wavelet transforms in turbulent flows and large eddy simulations (LES), with applications in wind energy and atmospheric boundary layer studies. Recent advancements in his work include deep learning-based scale-adaptive LES of floating wind farms, wavelet-based adaptive mesh generation, canopy-based immersed boundary methods, and phase-field modeling for multiphase flows.
Dr. Alam's academic journey began in Bangladesh, where he earned a B.Sc. (Honours) and M.Sc. in Mathematics from Chittagong University. In 1995, he became a Lecturer in the Department of Mathematics at Shahjalal University of Science and Technology (SUST), Bangladesh. He moved to Canada in 1998, completing an M.Sc. in Mathematics at the University of Alberta before pursuing his Ph.D. at McMaster University.
An interdisciplinary researcher, Dr. Alam is a faculty member of Memorial's Scientific Computing and Data Science program. His primary research interests lie in understanding turbulent fluid flows and their interactions with the environment. His work bridges fundamental investigations in turbulence with applied research, addressing challenges in atmospheric turbulence, wind energy, and nonlinear dynamics. His research group focuses on the development and testing of innovative numerical methods, including:
Dr. Alam's work has practical applications in understanding airflows around us in daily life--whether walking, driving, flying, or resting indoors. His studies on atmosphere-wind farm interactions and atmospheric turbulence in the wakes of ships, cars, aircraft, buildings, and mountains address pressing issues related to energy systems and climate change.
Through mathematical modeling and computational research, Dr. Alam aims to solve challenging problems in fluid dynamics to advance understanding of air circulation and its impact on our environment, offering solutions to mitigate the effects of climate change.

Climate change is one of the greatest challenges of our time, demanding a detailed understanding of atmospheric turbulence. Turbulence research often combines physics-based models with advanced numerical simulations, such as those used in large eddy simulation (LES). Emerging techniques, including wavelet transforms and neural networks, bring artificial intelligence (AI) into turbulence modeling, specifically in Scale-Adaptive Large Eddy Simulation (SALES) and Coherent Vortex Simulation (CVS). These AI-driven approaches open new possibilities for better capturing and understanding complex flow dynamics.
The effects of climate change are becoming increasingly evident in aviation, where stronger atmospheric turbulence is leading to more frequent and severe bumpy flights. This phenomenon costs the aviation industry between $200 and $500 million annually. Improving our understanding of turbulent atmospheric flows is therefore not only a scientific imperative but also an economic necessity. My research focuses on harnessing artificial intelligence to improve our understanding of the atmosphere - an environment in which we live and breathe every day.
I explore a wide range of fluid flow phenomena, using advanced numerical methods to solve problems in atmospheric turbulence. My primary focus is on multiscale modeling and data-driven numerical simulations of fluid turbulence. Turbulence is one of the most challenging problems in science and engineering, as it affects nearly every aspect of our lives. It limits vehicle fuel efficiency, contributes to bumpy airplane rides, impacts weather patterns and climate change, and influences clean energy technologies. Despite decades of research, predicting and controlling turbulent fluid flows remains a confounding challenge for scientists and engineers.
Consider the complexities of a hurricane passing over a city or a forest of giant wind turbines, where blades rotate at heights ranging from 100 to 500 meters above the ground. Representing such intricate systems in laboratory experiments is nearly impossible. Instead, researchers use turbulence modeling as a simplified representation of these complex dynamics. An open challenge in this field is defining which aspects of the dynamics should constitute a simplified model of such systems.
My interest in atmospheric turbulence is primarily motivated by the need to address pressing global issues, including the mitigation of greenhouse gases, the impact of urbanization, and the growing demand for energy. By combining AI-driven techniques with numerical simulations, my research aims to provide innovative solutions to these challenges, advancing our understanding of turbulence and its role in shaping the environment.
Wind energy is one of the fastest-growing and most promising renewable energy technologies globally. With its vast landmass, rich wind resources, and diverse technological expertise, Canada is poised to be a global leader in wind energy production and export. Newfoundland and Labrador, home to Memorial University, boasts the best onshore wind resources in North America. Leveraging this potential, wind energy research aims to train the next generation of engineers and scientists who will advance wind energy technologies and its integration into the energy grid.
Modern Computational Fluid Dynamics (CFD) techniques, combined with deep learning approaches, enable simulations of complex atmospheric interactions with wind turbines, providing critical insights for the optimization of wind farm designs. These methods are essential for efficiently exporting wind energy—whether through the production of hydrogen/ammonia or via transmission lines.
Understanding the interaction between wind farms and the atmospheric boundary layer is a cornerstone of turbulence modeling. A wind farm, composed of an array of wind turbines, extracts kinetic energy from the atmosphere and converts it into electricity. The aerodynamic behavior of these turbines, coupled with their wake effects, poses significant challenges and opportunities for optimization. Modern simulations reveal the role of vortices in turbulent flows, enhancing our understanding of energy capture and turbine efficiency.
Wind turbines in both onshore and offshore wind farms operate at heights between 30 m and 150 m, with typical turbine spacing ranging from 500 m to 700 m, depending on blade length. For instance, in an array of 41 wind turbines with rotor diameters of 126 m, each turbine's circular rotor disk harnesses kinetic energy from the atmosphere. These spatial and mechanical factors emphasize the need for vast land areas. However, through numerical simulations, my team explores innovative strategies to optimize energy production without expanding land usage.
One critical question in wind farm research is understanding how energy is transported by turbulence from the free atmosphere, where it originates, to the wind farm, where it is captured. This problem remains an open scientific challenge, requiring advanced numerical techniques and theoretical frameworks. My research program incorporates:
These tools allow us to address disagreements in the literature about the Coriolis force's effect on wake deflection and the impact of wind farms on local temperature. Some studies suggest wind farms cause localized warming, while others report cooling effects. My team's research provides new perspectives on these phenomena, informed by large-scale wind farm simulations.
The global hydrogen economy is projected to grow exponentially, with a 1000-fold increase in market demand by 2040. Meeting this demand requires rapid expansion of renewable energy installations, including wind farms in Newfoundland. To achieve the 1.5-degree climate change mitigation target, producing a quarter of the world's energy from hydrogen will necessitate substantial wind energy infrastructure. My research program directly addresses these challenges by investigating how wind farms can efficiently contribute to this energy transition.
My research program offers opportunities for undergraduate, graduate (M.Sc., Ph.D.), and postdoctoral researchers to work on cutting-edge projects in wind energy and atmospheric turbulence. Current projects are supported by NSERC and focus on:
Interested candidates are encouraged to contact me directly to discuss available research opportunities.
This research project focuses on some fundamental questions regarding atmospheric turbulence, particularly the physical mechanism behind the cascade and the dissipation of energy in turbulent flows. Briefly, LES is a numerical method for solving the Navier-Stokes equations. In other words, LES is a numerical method to understand the smoothness and other properties of the solutions of Navier-Stokes equations at high Reynolds number. An actual research project for students will be adjusted to the level of students' degree and background knowledge.
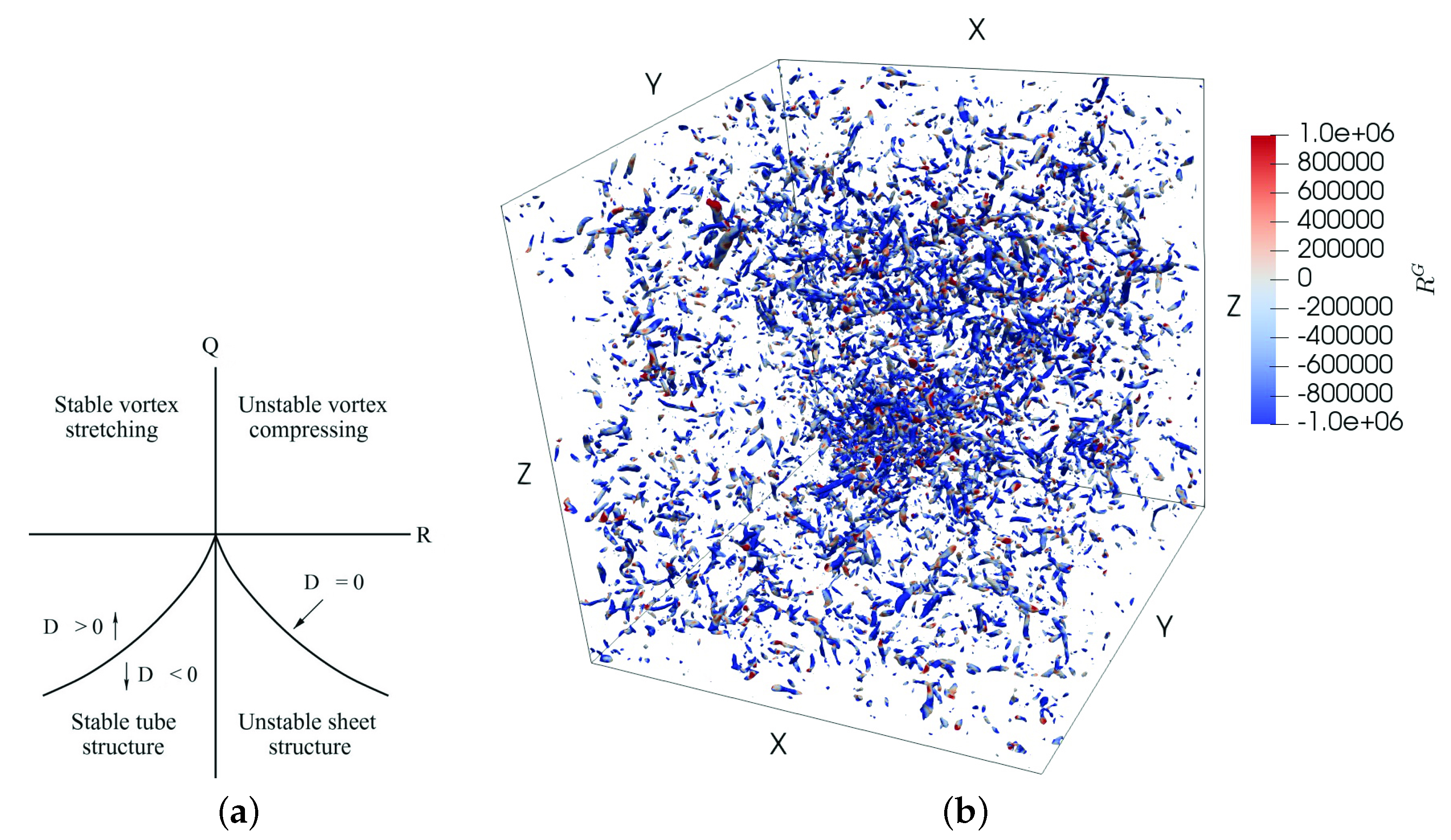
In the Figure (on left), the region with blue color indicates stretching of vortex tubes, and that with red color indicates vortex sheets. The dominancy of blue over red indicates the posibility of vortex stretching to be the dynamical mechanism. I use the LES method to understand whether the stretching of vortex filaments be assocated with the principal mechanical cause of dissipation in turbulent motion. Despite the evidences from LES that the energy cascade is driven by vortex stretching, a precise connection between the two has been openly debated. A new LES approach, which is based on vortex stretching phenomena, has been presented in this article.
Scientists and engineers believe that the Navier-Stokes equation can explain why we are not able to fly with an airplane smoothly if the atmosphere becomes turbulent. The Clay Institute of Mathematics declared a prize of one million dollars to be offered to whoever can mathematically prove the smoothness of solution of turbulence. It means that turbulence is not only an academic challenge, but also equally important in the aerospace and automobile industry.
One of my ideas include teaching theory of turbulence to talented students. I train my research team to be highly efficient in computational science and fluid dynamics, as well as proficient in code development using C++, Matlab, Python, etc. Interested students are encouraged to contact me directly.

Wavelets are special mathematical functions, often called mathematical microscope because wavelets discover hidden patterns underlying any function. Let y = f(x) be a function of x. A wavelet transform discovers hidden patterns of f(x) and we can focus on some important features of interest. Wavelet transforms share many aspects of neural networks (i.e. artificial intelligence and machine learning). Wavelets are useful techniques in computer science, data science, signal processing etc. My research on wavelet aim to develop wavelet-based adaptive numerical methods for solving partial differential equations.
A discrete wavelet transform employs a linear operator and focuses on the missing details - called wavelet coefficients. The modulus operator finds the active wavelets and captures the underlying non-linearity. In contrast, neural networks treat the missing details underlying a linear operator as biases and employ an activation operator, while optimizing the linear operator. Application of wavelets and neural networks to understand atmospheric turbulence is a primary element of my research program and student supervision. I have open PhD positions in this research direction.
This research project also investigates the theory of compressive sensing toward a new approach to turbulence modelling. In this direction, I study discrete wavelet transforms in order to incorporate two principles in turbulence modeling: sparsity, which concerns the significant dynamics of interest, and incoherence, which concerns fidelity of compressive sensing. The wavelet theory exploits the fact that turbulence is extremely intermettent, and thus, a turbulent flow posseses sparsity when expressed in wavelet basis. Incoherence extends the idea that a sparse dynamics must be spread out, just like a spike does.
Similar to traditional numerical methods, such as finite difference or finite element discretizations, machine learning techniques provide data-driven discretization of nonlinear partial differential equations. In Fluid Dynamics, the Navier-Stokes equations provide an open mathematical challenge, which is the lack of understanding the smoothness of the solution. Unsupervised machine learning, such as proper orthogonal decomposition (POD) and dynamic mode decomposition (DMD) are commonly used data-driven methods in fluid dynamics research. A potential question is whether DMD captures the solution manifold of the Navier-Stokes equation, thereby providing a hint for the smoothness of its solution and why a smooth fluid flow suddenly becomes violently turbulent. Such an understanding is crucial for wind energy and various other engineering and environmental situations.
Supervised machine learning can use neural networks to learn the discretization of nonlinear partial differential equations and has the potential to address many challenges of turbulence. Neural networks and wavelet transforms shares a lot of similar ideas. Understanding the connection between wavelets and neural networks is an open research area that leads to new data-driven approaches. There is a need to investigate how these techniques can provide a deep insight into atmospheric turbulence.
"Wavelet Transforms and Machine Learning Methods for the Study of Turbulence, Fluids 2023, 8(8), 224" discussed the ideas of deep learning and wavelet-based techniques.